The infection fatality rate (IFR) of COVID-19 is one of the most important parameters for mathematical models of the pandemic, yet it remains largely a mystery because we don’t yet know how many people have actually been infected. The IFR is the number of people who die from COVID-19 divided by the number of people who get infected. When you see the number of reported cases each day in the news, these reported cases include only people who have been diagnosed as having COVID-19 disease, or who have tested positive, but it does not include people who never get tested or are asymptomatic. Therefore, studies to assess the total number of infections are super important. This morning the results of a large-scale Stanford University study that tested for the presence of antibodies in the population of Santa Clara County, California were released.
- , , , , , , , , , , , , , , , ,
When conducting a large-scale community antibody test like this, the most important aspect of the experimental design is to make sure that the people selected for testing don’t self-select for the study. People who have reason to believe that they may have had COVID-19, or may have been exposed, will be vastly more eager to get tested than people who have no reason to think they may have had it. Ideally, you would either test everyone, or you should randomly select the participants without simply asking people to participate. If people self-select, this self-selection bias will result in a population of test subjects who are far more likely to have had the disease than the general population.
Today’s study is a very important one, and the researchers did a lot of other things right, but unfortunately they let participants self-select, so I believe that their reported results have overestimated the true prevalence in Santa Clara County. In this posting, I examine how to adjust their results to account for the self-selection bias.
How participants were selected
The following description of how participants were recruited is taken directly from their paper:
We recruited participants by placing targeted advertisements on Facebook aimed at residents of Santa Clara County. We used Facebook to quickly reach a large number of county residents and because it allows for granular targeting by zip code and sociodemographic characteristics. We used a combination of two targeting strategies: ads aimed at a representative population of the county by zip code, and specially targeted ads to balance our sample for under-represented zip codes. In addition, we capped registration from overrepresented areas. Individuals who clicked on the advertisement were directed to a survey hosted by the Stanford REDcap platform, which provided information about the study.
Basically, they put out a targeted ad on Facebook. Although it doesn’t say so here in the paper, I have heard second hand from people here in Santa Clara county that the ad offered a 10 Amazon gift card to participate. They targeted the ad to a subset of the population in each zip code.
They made substantial efforts to obtain a representative sample from the different zip codes and demographic groups within the county, and then after the proportions of participants didn’t quite match these distributions, they adjusted their results for this aspect of sampling bias. Their attention to this aspect of sampling bias was good. But they made no adjustments for self-selection bias.
All subjects’ blood were drawn for testing on 3-Apr-2020 or 4-Apr-2020 in three drive-through test sites in Los Gatos, San Jose and Mountain View.
The study’s results
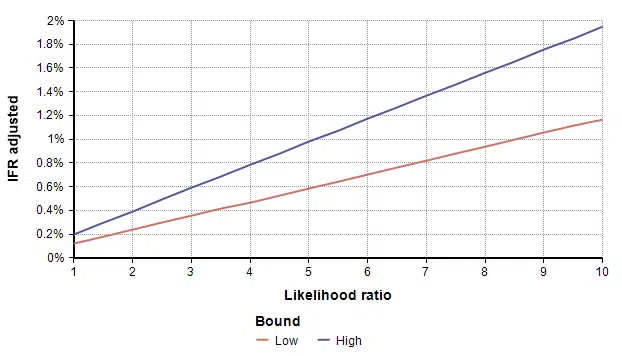
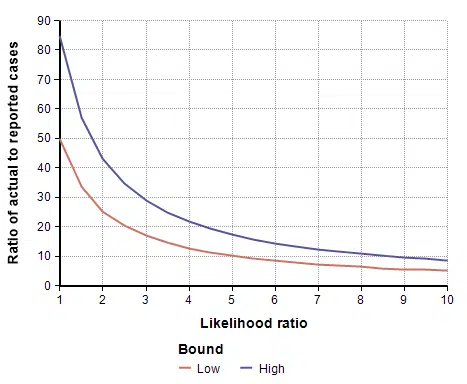
After eliminating some subjects for various technical reasons, the study ended up with 3,300 people with test results. Of those, 50 were positive test results, constituting 1.50% of the tests. After adjusting for demographic and geographic sampling biases, they adjusted this to an estimate of 2.81% positive. They then adjusted for the accuracy of the test (the actual accuracy is uncertain) to come up with a final estimate of prevalence between 2.49% to 4.16% percent, where the range is due to assumptions about the test’s accuracy. This prevalence translates to between 48,000 and 81,000 people in the county, which is 50-85 times the number of confirmed cases. This led to an IFR of 0.12% to 0.2%.
The results I just listed are directly from the paper. None of these results are adjusted for self-selection bias.
Self-selection adjustment
Suppose that people who have previously had COVID-19 are 10 times more likely to sign up for a test than people who have never been infected. This is called the likelihood ratio, which I’ll denote as L. In this example, L=10.
Let C denote whether a person has had COVID: C=true if they have, C=false if they haven’t. Let T denote whether that person enrolls in the test: T=true means they enroll, T=false means they don’t. With this notation, Bayes’ rule can be written as
[ odds( C | T ) = odds( C ) cdot L ]Where odds(C|T) is the odds a person had COVID-19 given that they take the test, and odds(C) is the odds a person from the general population had COVID-19. The study determined odds(C | T), whereas what we care about is odds(C), which doesn’t have the self-selection sampling bias.
The study estimated the prevalence, p, which is related to odds as odds(C|T) = p / (1-p). With some simple algebra, the true prevalence is obtained by multiplying the study’s estimate by an adjustment, alpha, given by
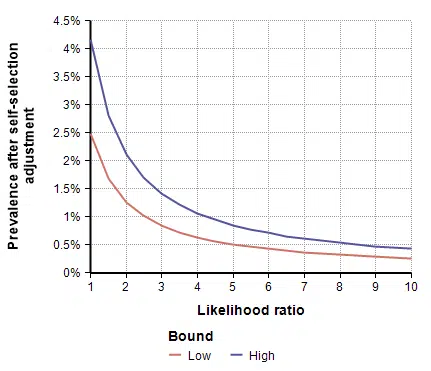
[ alpha = {1 over { L (1-p) + p }} ]This adjustment is shown in the following graph as a function of the likelihood ratio.
To adjust for self-selection bias, you need to estimate how many times more likely a person who had previously had COVID-19 would be to participate in the study, compared to a person who has never had it. This is the likelihood ratio. If you think that person would be 2.5 times as likely, use the self-selection adjustment for L=2.5 from the above graph, which is alpha=0.4, and then multiply the study’s prevalence number by 0.4, which yields a prevalence between 1.00% and 1.69%. You can also multiply by alpha to adjust the total number of infected people, which for L=2.5 is between 19,500 and 33,000. To adjust the IFR estimate, divide by alpha, which yields an adjusted IFR estimate between 0.29% and 0.49%. Adjusted values for these results are shown in the next four graphs as a function of likelihood ratio, the two lines showing the lower and upper estimates.
Estimating the Likelihood ratio
To adjust the study’s results, you have to estimate the likelihood ratio — how many times more likely someone previously infected would be to participate compared to someone never infected. Of course, this is also a big unknown.
Because the person considering whether to register doesn’t know whether she has COVID-19 or not, you might find the likelihood ratio to be overly abstract. It is easier to compare how much more likely it would be for someone who had symptoms at some point to participate in the study than someone who never had any symptoms. Of course, you might also want to consider the possibility that a person may be more likely to register because they know they had come into contact with someone else, or because their job makes them more vulnerable, etc. Because there are these other possibilities, I chose not to decompose the likelihood ratio into other estimations.
I live in Santa Clara County, and I was aware that the study was taking place. Many of my family’s friends were also aware that it was taking place, and we know of at least one person who tried very hard (unsuccessfully) to find the ad so that she could participate, because as she said, she had been sick and wanted to know if she had had COVID-19. Hence, based on my own experiences, my personal guess is L=5. But there is nothing magic about my guess, yours may differ.
Summary
The results from today’s study may lead some people to conclude that COVID-19 is no worse than the common flu. But this adjustment for self-selection bias show that this is not true. As the graphs above show, the prevalence drops off quickly when adjusted for even a small self-selection bias.
Understanding how many people in the population have had COVID-19 is an extremely important parameter for mathematical models of the pandemic. It is a critical piece of knowledge for determining how deadly a COVID-19 infection really is, for projecting hospital capacity and how many people may die, and for deciding when the economy can be reopened. Large scale tests of the population, like the Stanford study published today, help us estimate the prevalence of COVID-19 in the population.
When conducting a large-scale prevalence study, it is important to eliminate self-selection bias. When people are allowed to decide whether to participate in the study, those who have reason to believe that they are more likely to have had it will be more likely to participate. This may include people who had suspicious symptoms at some point, who know they were exposed at some point, or who work in situations that put them at greater risk of infection. In this article, I discussed how we can attempt to adjust for self-selection bias in the large-scale Santa Clara County study that was published this morning.
good point! have you had any reaction from the study authors?
Hi Paul. As far as I know, not yet.
I agree. Their methodology was deeply and unnecessarily flawed. You raised good motivators for self-selection: having felt ill, having been around someone who felt ill, being in a higher risk profession. Also, note the bias that is inherent in the method of using Facebook as the messenger with a brief period between posting on FB and the actual testing. We would need significant information on the other behaviors of people who use FB this frequently and whether they are more or less likely to have engaged in practices that would have put them at risk of acquiring the virus.
Back of the envelope “smell test”: 48,000 infections and only 69 deaths (as of April 17) is an infection fatality rate of 0.14%. This is inconsistent with Diamond Princess data, even if we adjust for age differences. Also compare with https://www.nejm.org/doi/full/10.1056/NEJMc2009316 in which they did UNIVERSAL screening of obstetric patients from March 22 to April 4 in NYC and found 15% positivity of SARS-CoV-2. Without lots of population-weighted adjustments we can interpret this as pretty good evidence of roughly 15% prevalence in NYC (say roughly 1.2 million infections) and roughly 9,000 deaths for infection fatality rate of 0.75%
Thank you for the reference to the obstetric patents study. I hadn’t seen that yet. Of course, the population of pregnant women would also have a ascertainment bias, since pregnant woman might have been more careful than other people, etc. But, like you, I have seen a lot of studies that have attempted to estimate the total number of cases in various populations, to get IFRs, and I have the same impression that the SC County study’s result was a far outlier. Your characterization as failing the back-of-the-envelope smell test is a good characterization.
The obstetric patient study is really interesting. I think the more revealing statistic there was the identification of 22 completely asymptomatic women, with only 7 showing symptoms (4 plus 3 who subsequently developed fever, though some may have been postpartum endometriosis). This suggests that only 25% of infected individuals may exhibit symptoms. Of course, the immune systems of pregnant women at term are “interesting” (e.g. activated CD69+ NK cells are elevated, for example), and they tend to be young and fit (I wouldn’t consider pregnancy to be a co-morbidity). I would therefore be surprised if that 3:1 ratio of asymptomatic versus symptomatic holds in a “normal” patient population. Finally, The one thing these women had in common was attendance at the same location (viz. their hospital) at pretty much the same time (this was a PCR test study, and therefore measures “active” infections). It is entirely possible that they became infected in the same time-frame, by the same individual or group of individuals, perhaps even the healthcare workers at the obs clinic). This may well make extrapolation of the 15% infection rate to the broader community inappropriate.
I’ve been getting a sense from studies like this one, the Runyun Li et al Science article on China asymptomatics, the Vo study, the Kenji Mizumotol Diamond Princess article, the Kimball et all CDC report for King Co. Wash. nursing facility, the Boston homeless shelter study, and others, that the percentage of the those get it but never develop symptoms is somewhere around 30%. There seems to be a fair amount of consistency emerging.
Dr. Chrisman,
Thank you for working through a potential correction to the selection bias present in Dr. Bhattacharya’s study. This model illustrates the impact that volunteer selection bias could have on the study result. As you suggest, your assumption of L=5-10 is fairly arbitrary and does not necessarily aid in demonstrating a more accurate prevalence estimate. The survey data from Dr. Bhattacharya’s study that reported previous symptoms of volunteers could be compared to Google’s symptom tracker for the county. This would provide a fairly accurate way to adjust for volunteer bias. I would be interested in seeing the effect that such an adjustment has on this model.
Regards,
Grace – very good point. They said they collected information participants’ symptoms, but they didn’t include that in their report. I think you are right that it would be useful for narrowing the actual amount of bias. Also, if we knew how many people actually saw the ads, versus how many signed up, it could help.
Lonnie, I believe you raised an excellent point regarding the bias.
However something bothers me in the first equation: L is defined as P(T|C)/P(T|C=false)
However Bayes:
P(C|T) = P(C)* P(T|C)/P(T)
So some redefinition of L may be needed here.
Yigal — Thanks for the feedback. Bayes’ rule can be written in terms of probabilities (as you did with P(C|T) = P(C)* P(T|C)/P(T)), or in terms of odds, as I did in the first equation. I used the odds form because I thought the likelihood ratio was a natural way to capture the relative likelihood of the two groups participating, and it already appears in odds form of Bayes’ rule. The odds a:b is the same as the probability a/(a+b), so it is possible to write it out in the probability form, using L = P(T|C) / P(T|not C).
Hi Lonnie, Spot on analysis, and looks like you might have extracted a more plausible number from the Bendavid et al data. I would also note that the serological test measures anyone who has ever been infected (i.e. in the last 120 days or so; though it can plausibly inform about recent infections [IgM] versus historic infections [IgG]), whereas the PCR test measures a snapshot of those that are currently infected. One would need to do some more fancy math(s) here, but this would also factor in to a better assessment of the real mortality rate. Remember that at least a couple of weeks of social distancing would have affected the numbers too…It is a shame that the authors have spoiled an otherwise useful study by not fully assessing these additional factors.
great work…much appreciated
Chris excellent analysis! Thanks
Thank you very much for the thoughtful analysis regarding self-selection bias!
I would only add that the tendency to self-select seems to me very likely to relate not only to (a) those who experienced COVID-19 like symptoms (perhaps those who had a bout with un-diagnosed influenza or something else) and (b) a known contact with a person known to be infected, but also those who (c) have frequented those places associated with known cases and/or (d) know someone who was infected even if they had no direct contact with such person since the outbreak began. These latter might be more generally characterized as those with a more acute interest in COVID-19, as compared to those who are less acutely interested in the outbreak.
As noted within the posted comments to the study itself, the sample population seems to have been subject to the state’s “Stay at Home” order during the conduct of sample collection, which seems to me to add yet another element of self-selection bias. One would have to be particularly committed to participation to violate the Stay at Home order to participate in a drive through collection of samples, even in the interest of science.
Given the described efforts to recruit a representative sample by zip code, the “Participant rate per 1,000 residents by zip code” shown in the Appendix to the study (page 14) seems to scream self-selection bias. Similarly, the sample skew as to sex and race indicate that the sample was far from representative.
Great analysis Lonnie. I too had the sense that doubling or tripling prevalence estimates based upon demographic data when such a small number tested positive is likely to significantly compound any errors generated by self-selection as opposed to randomized selection of participants. It was pointed out to me that because asymptomatic cases can be a significant portion of positive cases, this fact may ameliorate some of the self selection bias. I do not know how to integrate that factor into the adjustments the study team made.
Another important point, accuracy of the anti-body tests has been called into question and false positives in such a small number of participant positives may have greatly compounded errors of estimated prevalence predictions in the general population. Though the study attempted to make this adjustment, it is likely they erred on the side of their bias which was that case CFR was .06%.
Research bias is a thing. Many, most even, assume that a doctor at Stanford Medicine is without bias-that is a cultural privilege that can be exploited. Dr. Bendavid recently wrote an op-ed in the WSJ basically positing exactly the results he recently achieved in the Santa Clara County study (n=3,300) by citing the Vo Italy study (n=3,300). Is that a coincidence? Perhaps, but I think not. When a research study has a covert intent to prove a point, in this case that the CFR is so low that it is not worth repressing economic activity to keep people from dying, then it is important that all who read the study results be made aware of that bias-even if it is a bias that does not taint the results.
Dr. Bendavid has not revealed the funders of the study other than to cloak them in anonymity. Study funders must be identified.
The possibility that these authors had an agenda, that motivated them to achieve high prevalence rates and low IFR, is disturbing. But I think you are right that there are reasons to worry that this happened with this Santa Clara County study. In addition to Dr. Bendavid, John Ioannidis is also an author, who has published a few high profile op eds making similar arguments that the isolation measures & resulting economic shutdown where unwarranted because we don’t know enough to rule out the possibility that it might be not that dangerous. I am not in a position to make direct accusations that they intentionally distorted results because of an agenda, but I do have a uneasy feeling that this may have been the case.
The fact that study leaders Drs. Bendavid & Bhattacharya did not reveal their previous analysis of the Vo, Italy widespread test results stating infection prevalence was so high in Italy (3%) that CFR was only .06% in the discussion section of the SCC study indicates they did not want this fact revealed prior to publication. Drs. Bendavid & Bhattacharya also posited in the March 24 WSJ Op-Ed piece titled “Is Covid-19 as Deadly as They Say? that the total mortality of CV-19 in this country would be between 20K &40k, the high end be eclipsed in this country today.
Study results demonstrate confirmation bias.
I have to say that I am embarrassed to have made the above comment. I’ve thought about this more, and I don’t think there was any biasing agenda in the paper. I think the authors attempted an honest experiment, but had several methodological problems with the study’s design.
A wise self reflection. Calling out technical challenges in producing high integrity sampling is fair. Imputing perverse motivations on its authors due to a few speculative accusations is amateur. As it stands, the Santa Clara study has provided valuable insight at a time when any sense for the true progression of the virus is needed to support policymaking.
While I fully understand why you corrected yourself and applaud you for that, I unfortunately had the opposite conclusion. I initially thought the researchers were well-intentioned but poorly trained scientists who were a bit too eager to publish their results. But the same group did a similar study in LA county and went on a press tour. And their preprint could only be found in redstate.com, a far right website. (you will understand what I mean by far right when you go there). There is a somewhat innocuous explanation for this. (they released the preprint to hundreds of media websites and redstate was just one of them) But whatever their fundamental agenda may be, if you are too busy touting your own extreme headline-catching results, rather than academically defending and sharing your work, then it is malpractice at best.
I don’t have a PhD after my name but I do find it kind of a headscratcher that a criticism of the accuracy of a paper includes an estimate based primarily on “Many of my family’s friends were also aware that it was taking place, and we know of at least one person who tried very hard (unsuccessfully) to find the ad so that she could participate, because as she said, she had been sick and wanted to know if she had had COVID-19”.
You’re right that your guess isn’t magical but it is pretty comical.
Considering the universal hype and drama of the last couple of months over this pandemic and the frequent stories about asymptomatic carriers it seems possible, though how likely I don’t know, that the self selection went the other direction and freaked out people with no symptoms signed up disproportionately. That possibility seems increased by basing the selection on Facebook users which itself is something of a self selection process for easily panicked herd animals to begin with.
Below you indicate the fact the authors had expressed an interest in a similar Italian study as “disturbing” because it indicated they might have an agenda.
Is your consideration of self selection biases only being those that would have biased the results in one direction also “disturbing” to you?
It gives me an uneasy feeling in this case.
Either their numbers are right or wrong. The study in Italy is not the only one indicating mildly symptomatic and asymptomatic cases are far more widely spread than known so far. The same was found in Germany and on the East coast and IIRC other countries besides. We don’t know the answer yet.
But everybody has biases, including John Ryan, you and me. To start implying or worrying that someone elses is so much worse than our own based on nothing more than we disagree with them and their numbers are suspect because they have an agenda but we’re pure as the driven snow is the first and most important step to fooling ourselves. And as Feynman said we’re the easiest people to fool.
Brian — I accept your criticism. I work very hard to remain objective and avoid biases. I absolutely recognize, as you say, that we all have our own biases, and that I am no different. So when you let me know that I may be succumbing to a bias, I listen and I study that.
The alpha multiplier in my article works in both directions. If you do want to explore how the numbers change if the self-selection bias were to be in the other direction, this would correspond to L<1, and you can apply the same equation. Even a very small bias in the other direction results in a very fast increase in the prevalence.
I find it pretty hard to believe that the self-selection bias in this case would be in opposite direction, however. Part of my reason for this article was that I would like to find some way to squeeze some valid data from the results they collected.
Your point that it is still possible that we don't yet know the percentage of infected that never show symptoms is exactly the point I emphasized about why a study like this is so important. It is too bad they didn't do a better job at selecting participants.
HI Brian.. From personal experience I totally agree with your assessment that self selection may have gone the other direction. In Alberta where testing is now available, people are asked to register for testing based on a self assessment that includes runny nose and coughing.. for those who are freaked out, any sniffle is Covid. This might be just my availability bias but in my view there is equal likelihood that the paranoid signed up in droves.
Lonnie, very nice analysis. To be fair, Bendavid and his co-authors conceded that self-selection might be a problem: they wrote.
“Other biases, such as bias favoring individuals in good health capable of attending our testing sites, or bias favoring those with prior COVID-like illnesses seeking antibody confirmation are also possible. The overall effect of such biases is hard to ascertain.”
So yes, you’re right, the study is not methodologically rigorous when it comes to recruitment strategy, but the bias can work both ways. Perhaps the results actually undercount the percentage of people infected, because it drew a bunch of uninfected generally healthy “well worriers,” who confuse, say, their allergy symptoms with Covid. Or it tapped those who think, obversely, “Geez, I’m fine, but maybe I am infected but asymptomatic, and if I am, I can quarantine and then resume a normal life,” and it turns out that sort of person is uninfected.
Motivations can work multiple ways.
The other methodological complaint is that the test they scrambled to get has the potential for false positives. But, as with recruitment, there’s another side: the possibility of false negatives.
Methodological issues aside, we need more of these sorts of studies. I consider this study pretty crude, but nonetheless one of the essential first steps to really get to the bottom of this. Right now we are making huge consequential economic and societal decisions based at best incomplete data, and worst, on entrenched positions that range from “it’s like the flu” to “it’s the second coming of the bubonic plague.”
My guess — and I admit it’s a guess — is that it’s somewhere in between, with a CFR of about 0.3 to 0.5%, unadjusted, and way lower than that for people under 60 in good health. If it’s just seasonal flu level for those under 60 with no co-morbidities, then we should tell everyone in that age cohort to get back in business, and people over 60, and those with co-morbidities, especially asthma and COPD to do tough self-imposed mitigation.
It won’t be perfect, but what is? At least it won’t destroy the economy, which is what we are doing now.
Keep in mind that an IFR of 0.3% to 0.5% translates to about 660K to 1.1M deaths in the US if you just let if run its course. That isn’t counting the colateral deaths (due to lack of access to ICU facilities), which may be a bit larger than these numbers. In addition to IFR, the other factor is how many people would get the disease, and because there is no innate immunity in the population to COVID-19 as there is with the flu, there will be more cases. A quick way of estimating how many cases there would be in the absence of any human intervention (which is only a hypothetical, obviously) is to use (1 – 1/R0) as the fraction of the population will become infected — i.e., herd immunity. So with R0=3, that would be 220M people. The flu is a bit different in that regard since we have 50%ish of people who are vaccinated, plus some percentage who have innate or nearly innate immunity due to previous exposures in their lifetime. So we end up seeing 40M-ish people getting the flu each year.
With this in mind, it isn’t clear to me that the economy would be less destroyed if we were to let it run its course, even with an IFR of 0.3%.
Oops!! Forgot the extra zero! That will teach me not to do arithmetic late at night.
I meant 0.030% or around 100K+ deaths — including a pre-vaccine resurgence later in the year (though maybe it will be like H1N1, where we got a vaccine in 9 months). We’ll probably be south of 60K in this phase. So it will be worse than H1N1, but not 1918.
And again, we’d have to stratify that CFR by age and age/co-morbidity combinations. For someone over 70 with COPD, your chances may be 50-50 if you catch it.
The other thing I wanted to say about the Bendavid article is this — to do a demographic study right now to determine an IFR rate is very challenging. People are scattered and isolated. You don’t have time to do a cautious recruitment procedure within the walls of an institution. There isn’t time for the methodologically sounder, yet labor and time intensive approach.
To paraphrase Donald Rumsfeld, you do a study with the subjects you have, not the subjects you wish you had.
And, as I mentioned in my first post, the self-selection bias can work in multiple ways.
Finally, I find it interesting to see these Stanford guys get such aggressive pushback from various sources — the Twitter response, for example, was scathing. They clearly are in the camp of “this is not as bad as the Cassandras are making it out to be” and that seems to generate a lot of…..anger? Is anger the right word? A lot of the discussion has become more emotional — not yours of course, which was measured and thorough.
Sometimes I get the sense that the other camp — the “this is REALLY bad” camp– are fighting against the tide — the continuous adjustment downward of the IHME model, and what seems to be a 6-week “run its course” infection spread.
It would be great it the IFR was 0.03%, but the evidence it is not that low is pretty overwhelming. As you say, if it were that low, the number of deaths in the US would end up around 60K-100K in the absence of any protective measures (I’d say 66K is a good expectation). We are almost into that range now WITH extreme physical isolation measures and nowhere near herd immunity. Even the Bendavid study concluded that the percentage of people infected in Santa Clara County was <4.5%, a county that even one expects should have one of the highest percentages of previously infected in the country. So even here in Santa Clara County, we are a long ways from herd immunity. Your estimate of 0.3%-0.5% is still in the plausible range, although it does require a reasonably high percentage of unreported infected people to reconcile with current CFRs. For quite a while, my own median estimate was also around 0.3%, although lately as I've watch various studies come out, my estimate has shifted up from that slightly.
The IHME model has an explicit model of the impact of physical isolation measures. The reason their estimates have gone down is due to some extent because additional states adopted social isolation measures, hence when the fact they were adopted was entered, their prediction peaked earlier. I studied how that model works, and wrote about it here:
https://analytica.com/a-critique-of-the-univ-of-washingtons-imhe-covid-19-model/
It my be more detail than you wish to consume, but if you want to understand how they incorporate data on adoption of social isolation it may answer those questions. I also developed a model that has some similarities to IHME, which I’d invite you to read, which may be more relevant for you than my article on IHME:
https://analytica.com/forecast-update-us-deaths-from-covid-19-coronavirus-in-2020/
One of the things I’d like you to notice is the trend we were on before the effects of isolation measures kicked in. The US death rate was increasing at 22% per day very consistently. There is a ~3 week delay from the implementation isolation measures and the effect on death rate (since it takes people ~3 weeks from infection to death) . The 22% per day continued after I wrote that article up to 2-Apr, and then it started to bend, about where the effects of isolation measures would have started to show.
One statistical model that I think is worth watching is the University of Texas at Austin model at https://covid-19.tacc.utexas.edu/projections/. It extends the IHME model in two ways. First, they corrected a mathematical error with the way IHME projects uncertainty. And second, they incorporated cell phone tracking data, which enables it to incorporate real data about how well people are physically isolating. What I find really notable about this model is how well it has been tracking the actual trajectory. When you look at their April 1st projection through today, you can hardly distinguish the actual total deaths curve from the April 1st projection. Some of the same criticisms I made of the IHME model in my article apply to the UT model also (notably, the symmetry assumption), which would be relevant for the recovery phase, but nonetheless, I think this is probably the model to watch for now.
Thanks for that thoughtful reply, I will look at all of those.
If you’re right, then we are damned if we do and damned if we don’t. The virus has to run its course, now, or later, but eventually. Who will win the policy decision then?
If it’s Zeke Emmanuel, with his “it’s going to take 18 months,” at one extreme, we will destroy economic society as we know it. And even if we delay, say, another two months, and then open up, the consequences may still be catastrophic from BOTH a societal/economic AND and epidemiological point of view.
Or, on the other hand, do we just throw the dice and think, open up, and maybe hydroxycholoroquine-zinc works prophylactically, and maybe remdesivir works, or both work, and/or our standard of hospitalization care improves, and we can talk the people over 60 into sheltering, and so we roll the dice and hope it isn’t 600K dead, but more like 300K or, better yet, 150K.
Wouldn’t 150K be a victory if we DON’T crush our economy for the next 5 years, or more?
I guess I am in camp 2. Either way, life is both full of tradeoffs and, at bottom, tragic.
I know, it really stinks. I’m so sick of the economic impacts of the lock down, and would really love to be through this. The more I have studied it, the less I see it as a trade-off between economy and # of deaths, because the same things we need to do to return to a functional economy are the same things we need to do to squash the number of cases. I analyzed this in depth in my very long Triangle Suppression article:
https://lumina.com/forecast-update-us-deaths-from-covid-19-coronavirus-in-2020/
My colleague, Max Henrion, has recently also written an article, much shorter, with more focus on the post-suppression phase:
https://lumina.com/the-suppression-triangle-for-covid-19-what-happens-on-the-way-down/
My view is that getting the economy back requires us to squash the current outbreak first — getting the case load down quickly. A few other countries have proven it is possible. And then, once down, we enter a new world where we open things back up, but have to keep the case count squashed. I called in the “post-suppression stage”. Thomas Pueyo called it “the dance”. What we want to see is for the suppression stage to last only a few months, not 18. The post-suppression dance may last >18 months, but with a functioning economy. How we are doing to keep R<1 during the dance is the big question to be thinking about now.
It’s possible to be sensitive to that colliding venn diagram, where you’re concerned about suppressing COVID-19, worried about the economic impacts, and concerned about government intervention/suppression/imposition. However, if we don’t suppress (r<<1) significantly first, what are the consequences of reopening, and seeing a large second wave of infections. Most of us on the epidemiological side of things are concerned about that second wave, especially in the more rural areas that haven't yet spiked.
I fully anticipate we'll see areas reexert high case loads, and I wouldn't be surprised to see new epicenters of infection. What will be devastating is if those are more rural, next time, where small hospitals cannot care for them. a 45 minute ambulance ride with a crashing patient on a ventilator tends to take a high toll on EMS, as well as patients in that setting.
I'd be MUCH happier to see us wait, ignore the Kemp experiment in Georgia, and for that matter, the Dan Patrick/Abbott experiment in Texas, and let at least another 4 weeks go by to see what the recognized case loads are at that point, establish if the curve's really flat (hello, S. Dakota?, Georgia?) and then demonstrate some rational approach to rolling things out in a controlled and thoughtful manner. The process of opening everything in 72 hours (Kemp) is asking for a spike.
And while we're at it, the concept voiced by Dan Patrick, Lt Gov of Texas, implicates he's ready to sacrifice an unknown number of his citizens (although he tags it at 500) to preserve the economy. Part of his rationale, stated or unstated, is that since the predictions are no longer so dire, the emergency was overblown. In fact, had we not undertaken draconian measures to encourage self-isolation, social distancing and suppression of group gatherings, I propose we'd have been much high in the number of cases, although we'd likely still be far behind on testing even symptomatic patients, and the death toll would be staggering. In other words, we were successful enough in our efforts that select politicians want to say the efforts were unnecessary, as a self-fulfilling prophecy that the pandemic's been overblown all along.
Thank you for sharing such a good information. Very informative and effective post. Keep it up!